Key exchange and Zero-Knowledge-Proof

In the previous articles, titled Explaining Zero-Knowledge-Proof strategies in an abstract manner through a hypothetical story and How a couple of courses in Physics lead to the creation of HexHoot, we did briefly discuss Key exchange and Zero-Knowledge-Proof. However, I think it is quite important to describe, in detail, how these come into play in the context of HexHoot.

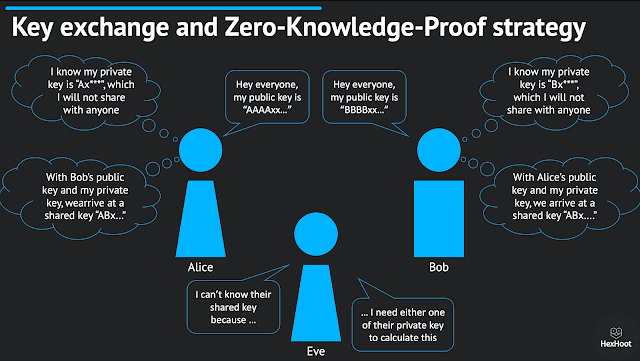
The principle behind Key exchange can be summarized in one figure, as shown below. If Alice and Bob would like to communicate with each other, they log in to HexHoot with an automatically generated private key. Then they share their public keys with each other, which could even be over a public channel, like posting a blog or shouting out aloud. Once they exchange the public keys, using one person's public key and the other person's private key, they can arrive at a shared key; it does not matter which private key or public key is used, they both arrive at the same answer. They can now encrypt their messages with this shared key, which lets them communicate securely.

However, an eavesdropper, Eve, can not arrive at this shared key that is used for encryption. She needs at least one of Alice's or Bob's private keys to calculate the same. Therefore, even if Eve tries to get in the middle and attempt to read the messages sent between Alice and Bob, she can not decrypt the messages.

Now, at this point, if you are not with me on why this can be considered a Zero-Knowledge-Proof strategy, let me explain. Here, both Alice and Bob act as provers and verifiers simultaneously. Alice and Bob have private keys, which are essentially their pass-codes, and they want to prove that they have their private keys without actually revealing the private keys. They both share their public keys, but neither Bob nor Alice can calculate the latter's private key using this public key. However, they can both arrive at a shared key using which they can encrypt and decrypt messages. In other words, Alice can verify that Bob owns his private key because Bob can decrypt the message that Alice sends and respond back with the same encryption; and vice-versa.

No matter what the communication channel is, this method can help in authenticating users without the use of a central system. All we need is an agreement on the protocol that we use.